In our previous post, we covered Desmos tips for SAT, specifically on using the Desmos SAT calculator to solve single-variable equations. In this post, we’ll dive into a more advanced topic: solving single-variable equations with unknown constants. Utilizing the Desmos SAT calculator and its slider tool, you can efficiently manage these problems on the Digital SAT, enhancing your overall SAT math performance.
What Are Single-Variable Equations with Unknown Constants?
Single-variable equations with unknown constants contain both a variable (like x) and a constant parameter (like p, c, or m) that affects the equation’s solutions.
The problem below is one example of a single variable equation with an unknown constant. This single variable equation is a linear equation with an unknown constant “p.”
How to Solve Equations with Unknown Constants Using Desmos SAT?
Question:

Follow these steps:
Step 1. Enter the Equation
Type the equation into Row 1 of the Desmos SAT calculator. Since this problem involves an unknown constant like “p,” Desmos SAT will prompt you to create a slider for it. Click the constant highlighted in blue to add the slider.
2. Set the Slider Range
Click to the left and right of the slider icon to adjust the slider range if needed. For this example question, the answer choices range from 0 to 4, so the default setting of -10 to 10 works well here.
3. Check the Solutions
Use the slider to check different values for the constant and see how they affect the graph. You can also set the slider to specific values. This is a great tactic on multiple choice questions like this one, because you can quickly check each answer choice by entering a precise value for “p.” 
The correct answer is Choice B. When we set the slider equal to 1/7, the Desmos calculator does not produce any vertical lines. As we’ll remember from the last post, vertical lines indicate solutions. If Desmos produces no vertical lines when p = 1/7, that means that when p = 1/7, this equation has no solutions. The correct answer is therefore B, 1/7.
Video Tutorial: See Desmos in Action
Check out this video where we demonstrate the step-by-step process of solving single-variable equations with unknown constants using the Desmos SAT calculator. Follow along to master the slider tool and efficiently tackle similar problems on your SAT:
Additional Practice Problems with Desmos SAT
Question 1: How Do You Solve a Quadratic Equation with an Unknown Constant?
This problem features a quadratic equation with an unknown constant “c.” The approach for solving this quadratic equation with Desmos SAT remains similar to that of linear equations.

Solution:
Choice C is correct. The question asks us to identify the value of c for which the equation has one solution. Because this is a multiple choice question, we find the solution by plugging in each answer choice for “p.” -25 is the only value that produces one vertical line. Therefore Choice C must be correct:
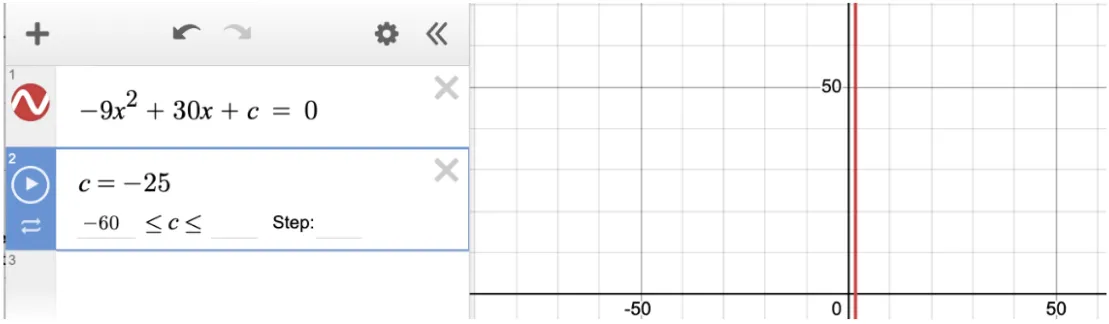
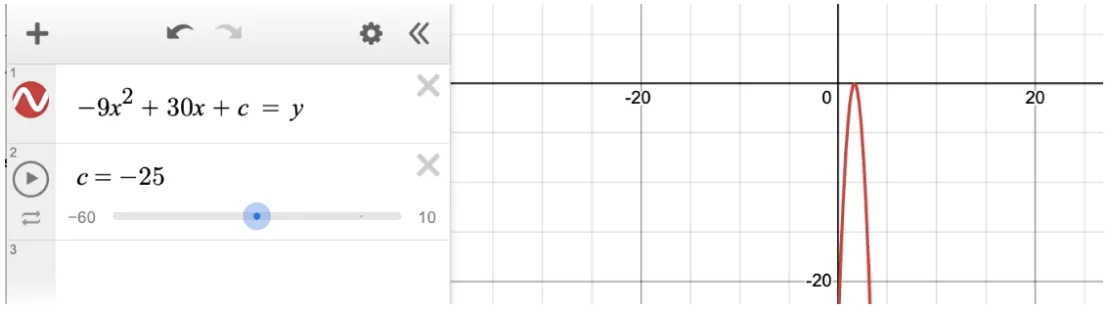
Question 2: Quadratic Equation with an Unknown “b” Value
This is a quadratic equation where we need to determine the value of “b”. This equation is not a multiple choice question, so it is probably best solved using a function
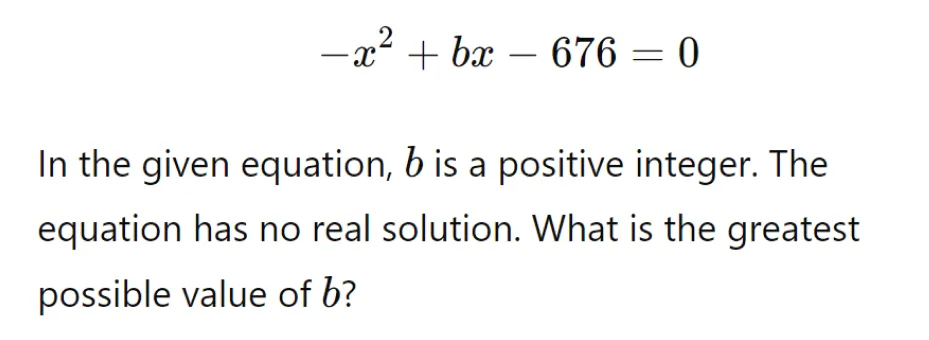
Solution:
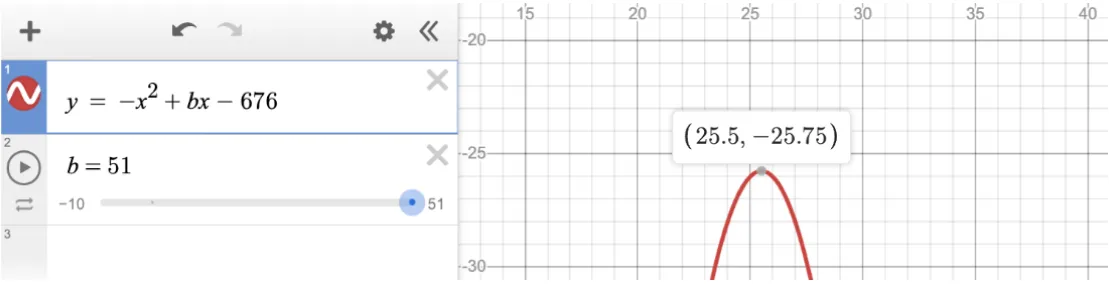
The correct answer is 51. Using Desmos SAT, replace the zero in the original equation with “y” to observe the graph. The equation has no solutions when b = 52. The problem states that the equation has no solutions. We can use the slider to see that the quadratic has no solutions whenever b is less than 52. The greatest integer value of b that yields zero solutions is therefore 51.
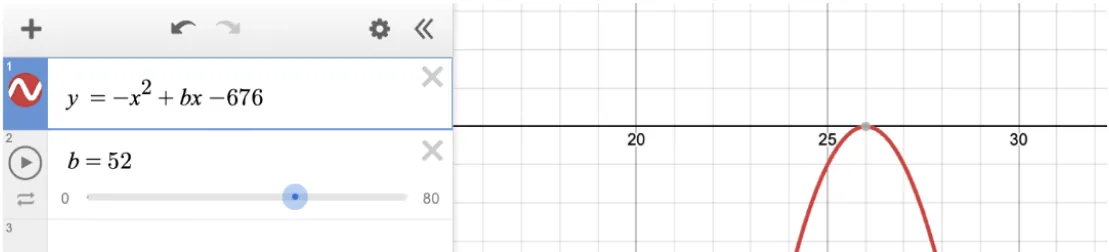
When b = 51, the function has no solutions, because it is an “open down” parabola with a vertex at (25.5, -25.75).
Question 3: Single-Variable Linear Equation with Unknown “m”
For this linear equation, we need to test different values for “m” to identify the correct solution.
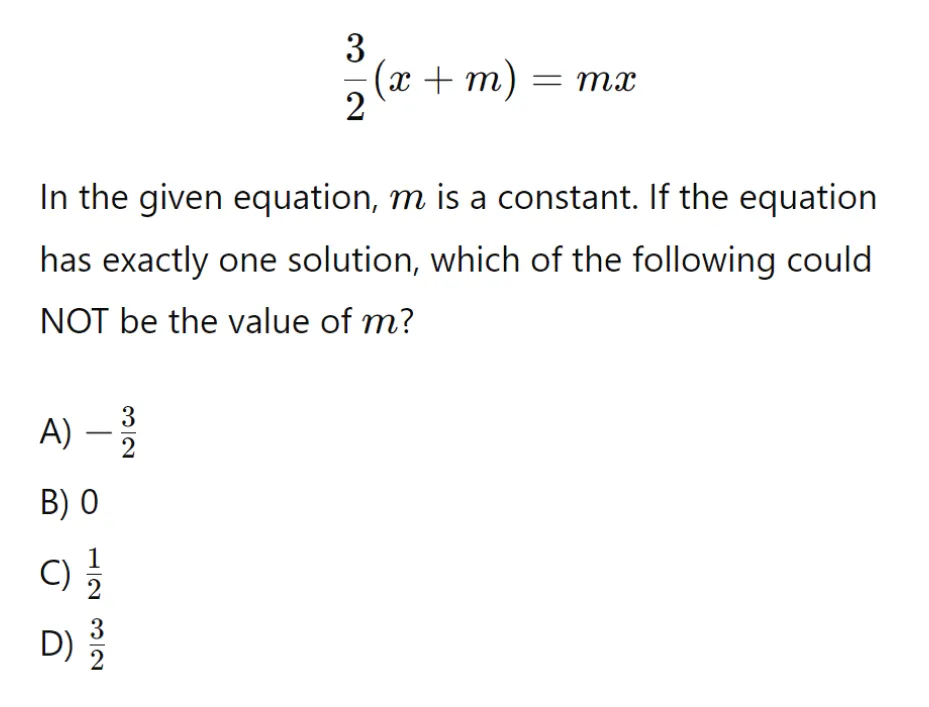
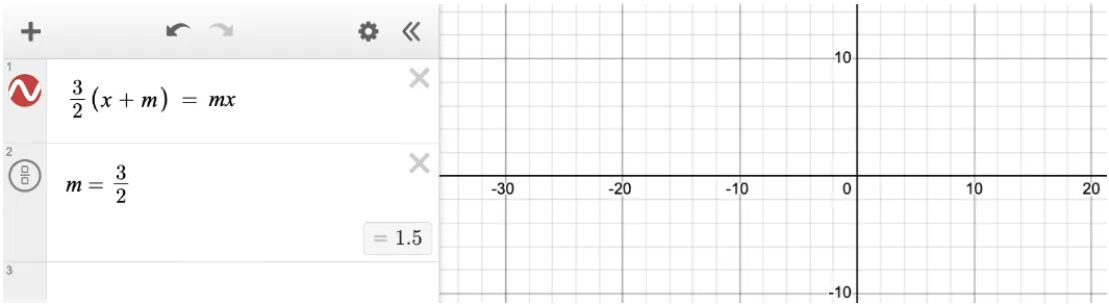
Solution:
The correct answer is D (3/2). The question indicates that the equation has one solution. Testing each answer choice in Desmos, we can see that every choice except for 3/2 produces one vertical line. Choice D does not produce a vertical line. This means that when m = 3/2, the equation has either infinite solutions or no solutions. With a bit of algebra we can see that when m = 3/2, the equation has no solutions. In either case, the answer is D, 3/2.
Key Takeaways for SAT Math Success
- Desmos SAT Calculator is an essential tool for solving equations with unknown constants.
- Use the slider tool to test different values quickly and find accurate solutions.
- Remember, while Desmos helps with the calculations, a strong foundation in math is crucial for scoring high on the SAT.
Frequently Asked Questions
Vertical lines indicate solutions to equations. Each vertical line represents one x-value where the equation is true. No vertical lines means no solutions exist, one vertical line means one solution, and multiple vertical lines indicate multiple solutions.
Yes. The Desmos SAT calculator is built into the Digital SAT testing interface and provided by College Board for all test-takers to use.
Use the slider method for multiple choice questions where you can test each answer choice quickly. Use the graphing method (converting to y= form) for grid-in questions or when you need to understand the solution behavior visually.
No solutions means the equation is impossible (produces no vertical lines in Desmos). Infinite solutions means the equation is always true for all x-values. Both can appear to have “no vertical lines,” but infinite solutions occur when the equation reduces to an identity like 0=0.
Check your answer choices first. Set the slider range to include all answer choice values. The default -10 to 10 works for most problems, but you can click the range numbers to adjust them.
Yes. Desmos handles both types using the same slider tool approach. The only difference is that quadratics may show 0, 1, or 2 vertical lines, while linear equations typically show 0 or 1 vertical line.
Make sure you’re using a lowercase single letter for your constant. Desmos automatically creates sliders for lowercase letters (a-z). Double-check for typos in your equation.
Yes. Convert the equation to function form (replace the constant value with “y”), then use the slider to find when the graph shows the desired property (no solutions, one solution, etc.).
Looking Ahead: Desmos Tips for SAT, Part 3
In the next part of this series, we’ll explore how to solve systems of equations using Desmos SAT. This powerful tool will help you identify intersection points for multiple variables, providing another strategy to excel on the SAT math section.
Prepare for the SAT with MentoMind
Ready for more practice with Desmos SAT? Check out MentoMind, where you can access:
- 3,500+ SAT practice questions with detailed ICE-based explanations
- 11 full-length adaptive digital SAT tests that mirror the real exam
- AI-powered chatbot that provides personalized study tips and identifies your weak areas
- Section-by-section analytics to track improvement on Reading & Writing questions
- Diagnostic tests that establish your baseline and create personalized study plans