In our previous post, we covered Desmos tips for SAT, specifically on using the Desmos SAT calculator to solve single-variable equations, including those with unknown constants. We also introduced basic Desmos tools like the slider feature. In this blog, we’ll focus on a new problem type: solving systems of equations using the Desmos SAT calculator.
Solving Linear Systems of Equations with the Desmos SAT Systems of Equations Calculator
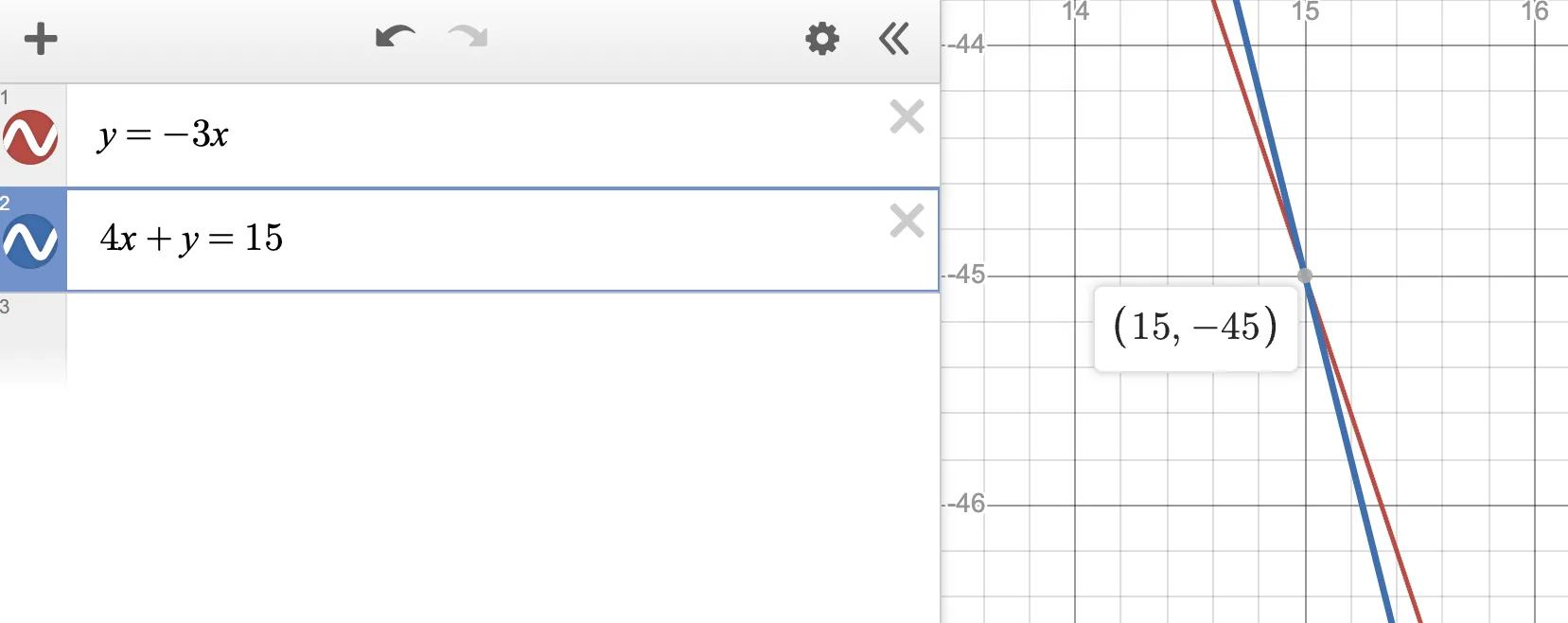
Linear systems of equations consist of straight-line equations. The solution to a system of equations is the point where these lines intersect. The Desmos SAT systems of equations calculator allows you to find this solution quickly.
Here is an example question.

Steps to Solve Linear Systems Using the Desmos SAT Calculator
- Enter the System: Enter the Given Equations into Rows 1 and 2 in the Desmos expression list.

- Find the Solution: Use your cursor to locate the point of intersection between the lines. The Desmos SAT calculator will highlight the coordinates of the solution.

Choice C is correct. The question asks us for the x value of the solution to the given system. By simply entering the equations into Desmos, we can see that line point of intersection occurs at (15, -45). The solution is the x-value, which is 15.
See Desmos in Action: Solving System of Equation
Check out this video where we demonstrate the step-by-step process of solving system of equations using the Desmos SAT calculator.
Solving Mixed Systems of Equations with the Desmos SAT Calculator
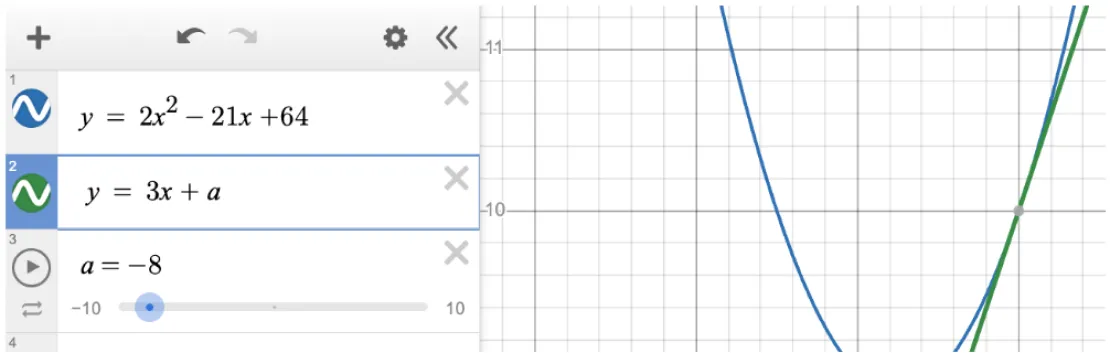
The equation below is a mixed system, because it contains two types of functions – one linear and one quadratic. An additional challenge is that this problem also contains an unknown constant, which we covered in the last post on mastering equations with unknown constants. The Desmos sat calculator is especially helpful in solving these by using its sliders and graphing capabilities, making it a great tool for those looking for Desmos tips for SAT.
To Solve a Problem Like This:

Follow These Steps
- Enter the System: Enter the given equations into Rows 1 and 2 of the Desmos expression list. When prompted, add a slider for the constant “a.” This constant is the y-intercept for the linear equation in this system.

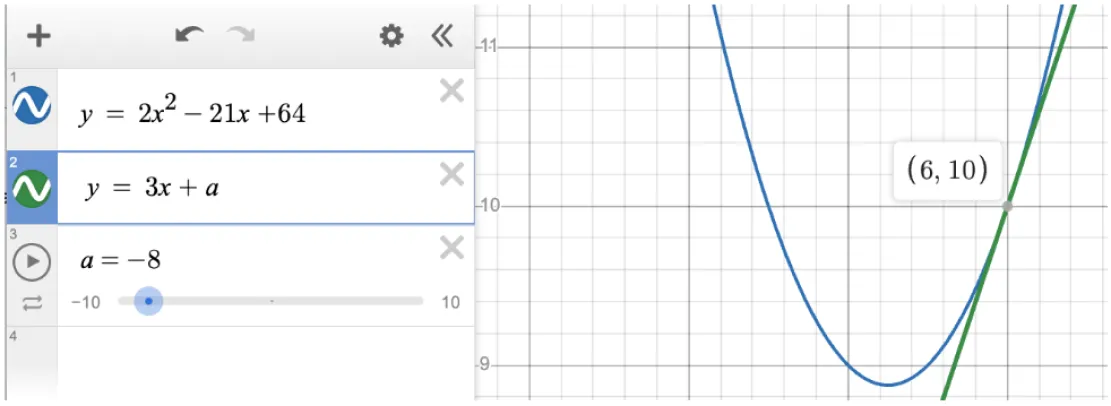
- Solve for the constants: .The question states that the given system has one solution. Use the desmos slider to change the value of a until the lines cross at one point. We can see that these lines cross at one point when a = -8.

- Identify the Solution: The “a” value that produces 1 solution is -8. However, this is not the answer to the question. The question asks us to identify the value of x for the solution to the system. Hovering over the point of intersection with our cursor, we can see that this value is x = 6.

This is another case where strong math skills are crucial. Probably, the Desmos solution is faster than working through the algebra. However, you still need to interpret the system to find the correct solution. You must understand how systems work and what the question is asking you to find. If you do, Desmos can help you to swiftly identify the correct choice.
Additional Example Problems with Desmos SAT Calculator Solutions
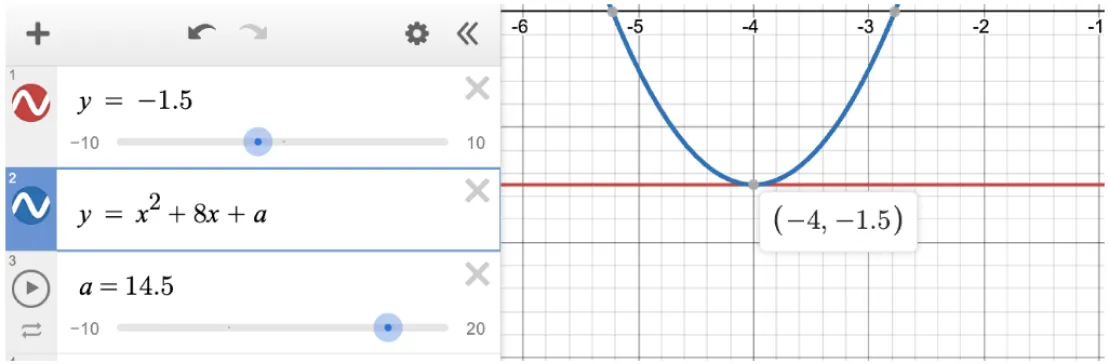
Question 1: The problem below is a mixed system. In this case, the linear function is a horizontal line. It is a straight line in the coordinate plane with a slope of zero and a y-intercept of -1.5.
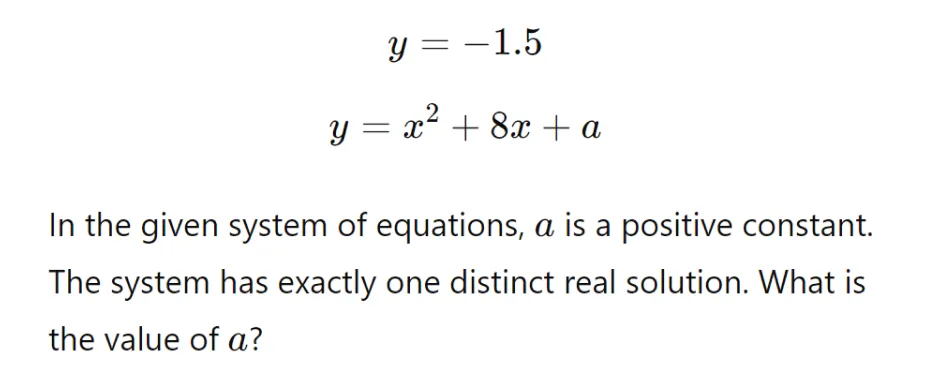
Solution:The answer to this equation is a = -14.5. Applying the Desmos slider, we can see that -14.5 is the value of a that produces one solution. When a = -14.5, the graphs of the functions in this system intersect at only one point.
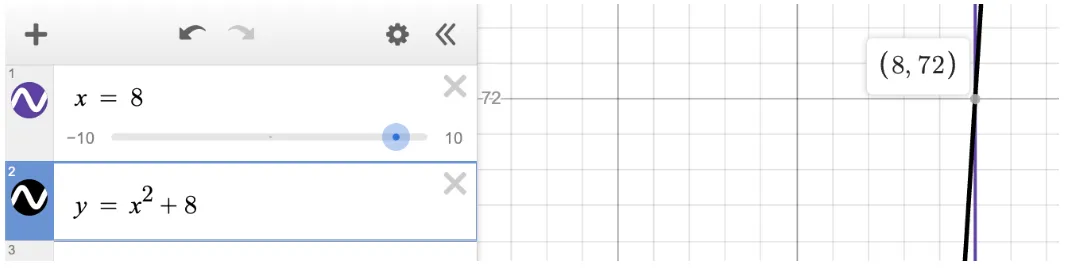
Question 2: The problem below is another mixed system. This system contains a vertical line at x = 8 and quadratic equation that is symmetrical about the y-axis with a y-intercept of 8.

Solution: Choice D is correct. There are no unknown constants, so no slider is required. All we have to do is plug both equations into the Desmos SAT Calculator, and find the y-value of the intersection between the graphs. These lines intersect at (8, 72).
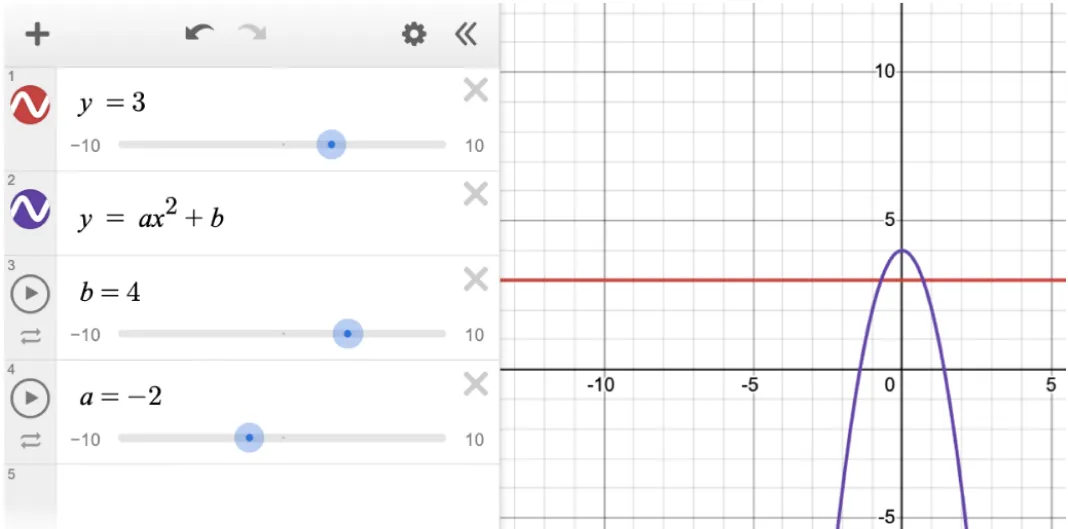
Question 3: The problem below is a mixed system. In this case, the quadratic equation contains two unknown constants. Because this is a multiple choice question, we can plug in each answer choice, using sliders for the constants a and b.

Solution: Choice B is correct. When a = -2 and b = 4, the graphs intersect at two points. This indicates that the system has two solutions.
Conclusion: Mastering Desmos SAT Tips with the Graphing Calculator
Mastering the Desmos SAT calculator for solving systems of equations is crucial for enhancing your SAT math performance. Whether you’re working with Desmos linear systems or mixed systems, utilizing the calculator’s powerful features will help you solve problems with speed and accuracy. Incorporating these Desmos tips for SAT into your study routine can significantly boost your performance.
For more in-depth Desmos tips for the SAT and to continue your journey of mastering SAT math, check out the previous parts of our blog series: Part 1 and Part 2. At MentoMind, you can not only explore these resources but also practice with full-length digital SAT tests. Our platform is packed with tools like the Desmos SAT calculator to help you elevate your skills and achieve your target score. Don’t miss out—start your free trial today and experience firsthand how MentoMind can transform your SAT preparation!